二进制
我们从机械计算机,升级到了机电计算机,再到了电子计算机,逐渐希望用“电”来代替“机械运作”进行计算。减少了机械设备,就能降低计算机的物理磨损,可以使计算更加可靠,也变得更快。
还记得莱布尼茨的步进计算机吗?它用10个齿的齿轮来代表十进制数进行计算。然而,当我们试图用电流强弱的程度来表达十进制的时候,却发现受到的干扰太多了(比如计算机电池要没电了,或者电源电压不稳等等)。为了解决这个问题,人们尝试过制造五进制,三进制的电子计算机,却依然不能进行可靠的计算。于是,可以只用电流“开”,“关”两种状态进行表达的二进制计算机被设计了出来。
二进制只有“真”或“假”两个值,也可以表示成“1”或“0”。当电路闭合,电流流过的时候,表示“真”;电路断开,没有电流流过的时候表示“假”,这样的方式很难受到外界的干扰,可以让我们的计算机工作的更加稳定!
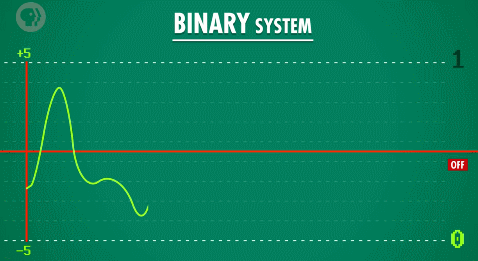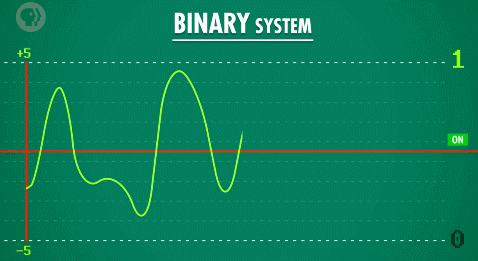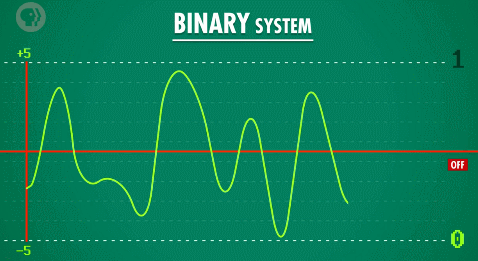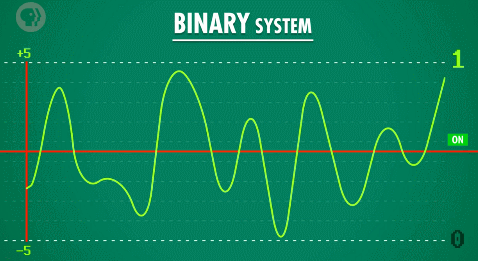
逻辑门电路
使用二进制的另外一个原因是,有一整套的数学计算的方法,来专门处理“真”或“假”,那就是布尔代数。它是以19世纪的英国数学家 George Boole 的名字来命名的。
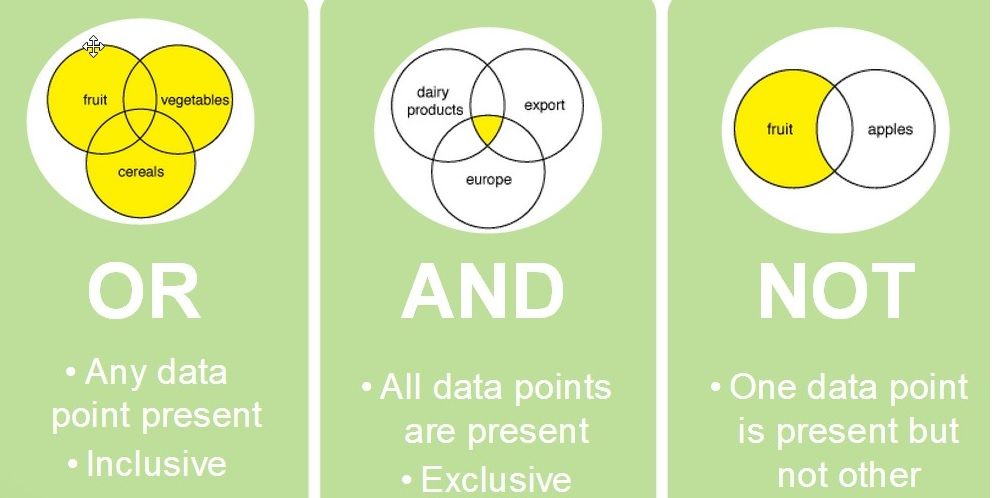
Boole 一直致力于用一种类似常规代数的计算方法,来处理亚里士多德哲学中的逻辑问题。对比于代数中的加减乘除,布尔代数也有三个基本计算方式,那就是“与”,“或”,“非”。让我们分别来了解一下,并用晶体管制作出这三种基本门电路:
“非”门
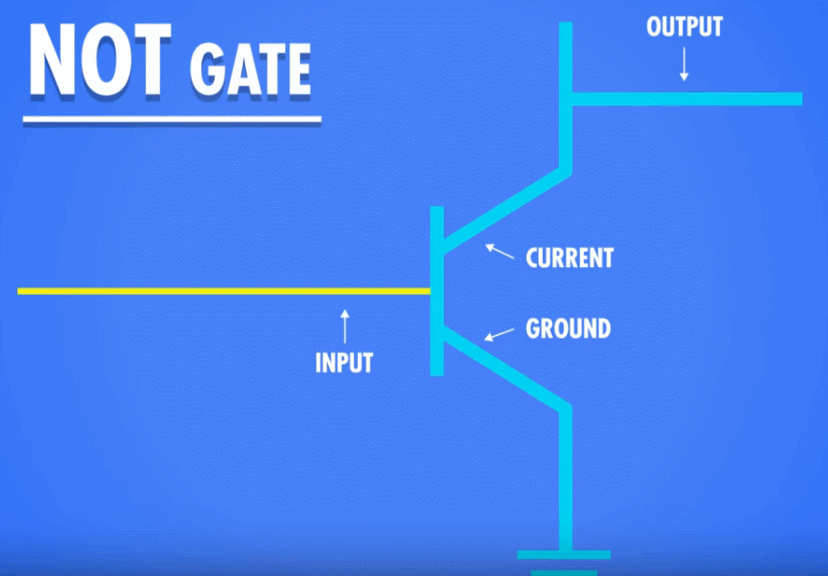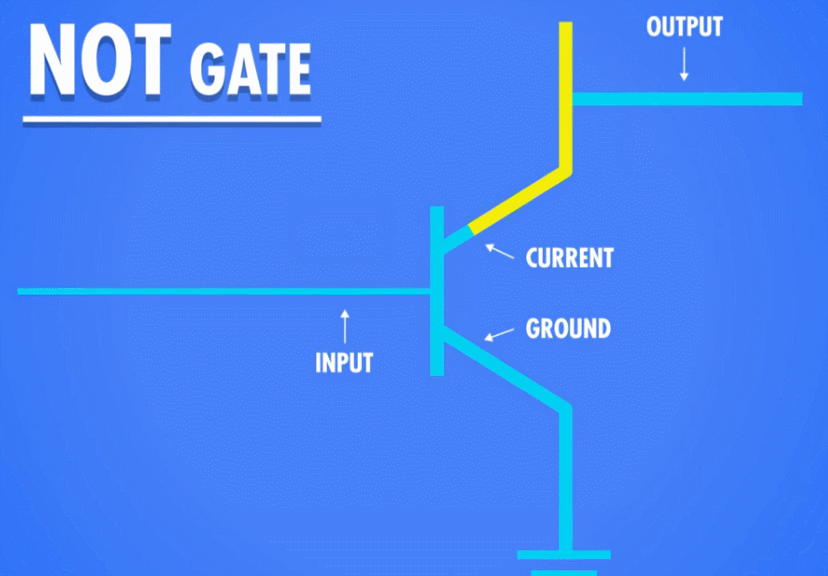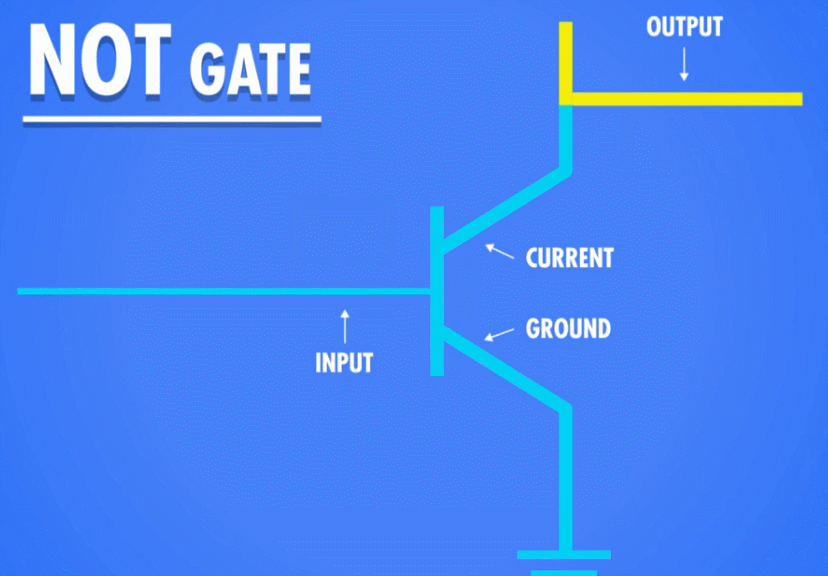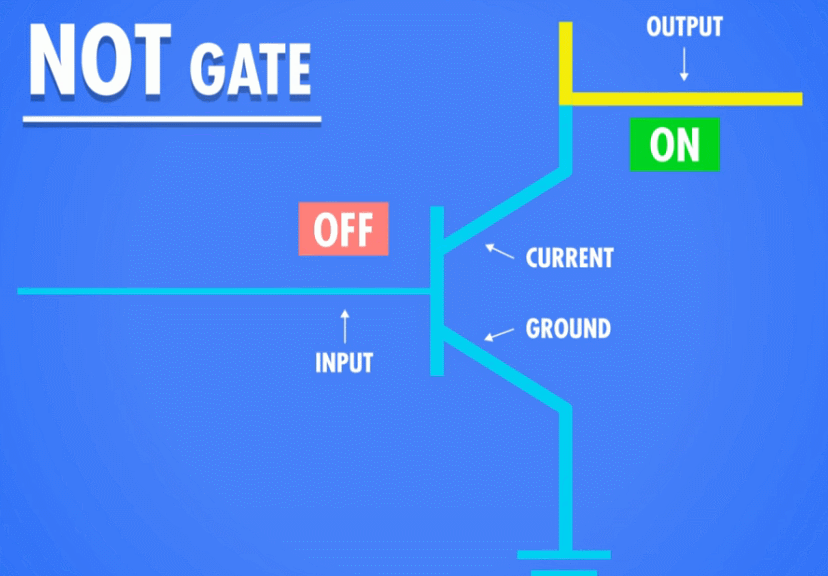
“非”运算非常简单,它拥有一个输入和一个输出,运算结果就是把原来输入的结果反转:

前面提到,晶体管类似于一个水龙头一样,当接通控制电路的时候,半导体导电,输出就有了电流;断开控制电路的时候,输出就没有电流。
为了制造“非”门,我们需要将晶体管的输入输出极调整一下:我们将晶体管的一极接地,另外一极接通输出电路。这样,当我们接通控制电路的时候,电流就直接流入地面,而不会流过输出电路,只有断开控制电路的时候,电流才流过输出电路。想象成我们把水龙头安在了一个大的排水管上,关闭排水管,家里的水管里才有水;打开排水管,家里的水管就没水了。
“与”门
“与”门需要两个输入,只有当着两个输入同时为“真”的时候,输出才为“真”,只要任意一个输入为“假”,则输出就为“假”。
比如:奥巴马是美国总统与奥巴马是黑人,结果为真;奥巴马是美国总统与奥巴马是白人,结果就为假。

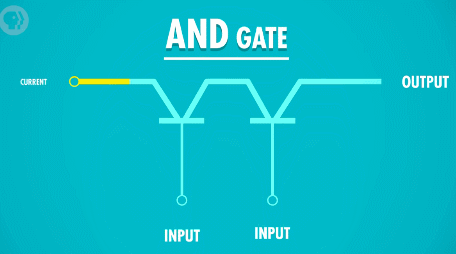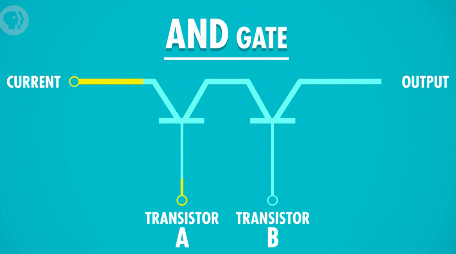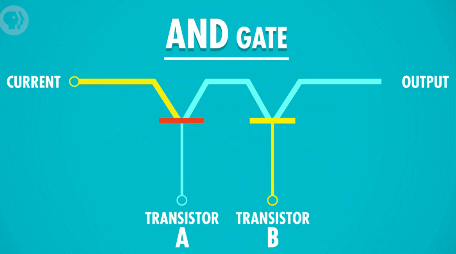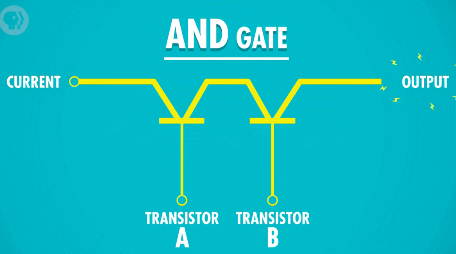
制造“与”门电路,我们需要将两个晶体管串联起来。这样,用两个晶体管的控制电路作为输入,就必须两个输入端都接通,输出电路才有电流流过。
“或”门
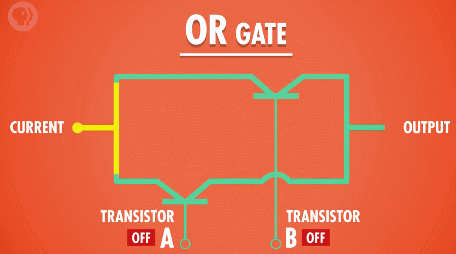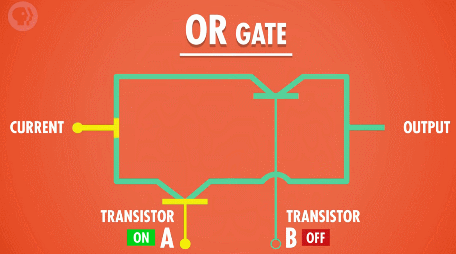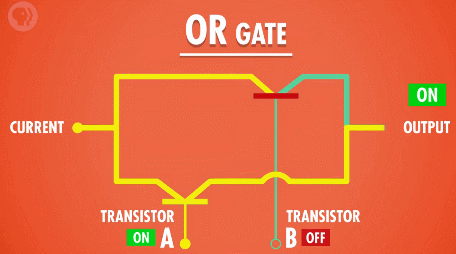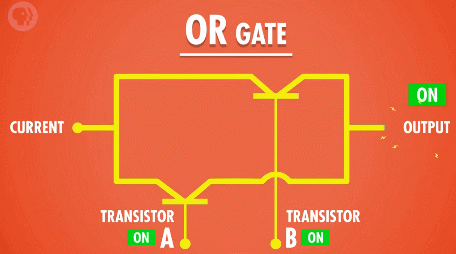
“或”门同样需要两个输入,并且只要任意一个输入为“真”,则输出就为真;只有当两个输入都为“假”的时候,结果为“假”。
同样的例子:奥巴马是美国总统或奥巴马是白人,结果为真;奥巴马是韩国总统或奥巴马是黄种人,结果为假。

制造“或”门电路,我们同样需要两个晶体管,只不过这次我们需要加一些额外的线路将它们并联:
抽象
在真实世界中,即使是职业的程序员或工程师也并不总会去关心电流是怎么在计算机里流动的。人们往往会将常用的零件组装成一个粒度更大,使用更方便的工具,而不需要再去关心零件的细节,这样的过程就叫做“抽象”。
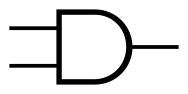
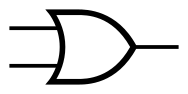
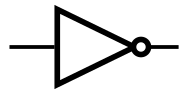
同样,我们现在做出了“与”,“或”,“非”三种门电路,人们抽象出了三种符号来分别代替它们:
“异或”门
除开这三种基本操作以外,还有个非常有用的布尔运算教做“异或”,异或和或运算非常像,当任意一个输入为“真”的时候,输出为“真”;不同点在于,当两个输入都为“真”,或者两个输入都为“假”的时候,输出为“假”。换句话说,只有当两个输入状态不一样的时候,输出为“真”;两个输入状态一致的时候,输出就为“假”。

利用晶体管来制造“异或”门电路就相当复杂了,还好我们可以用抽象出来的工具:“与”、“或”、“非”门来组装它:
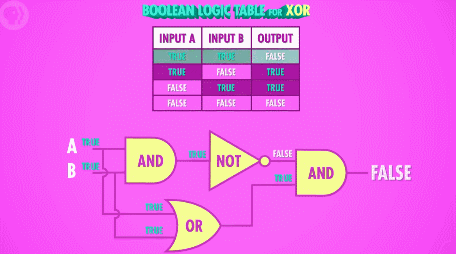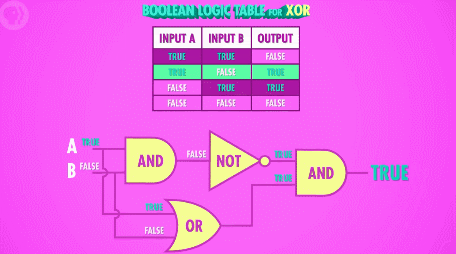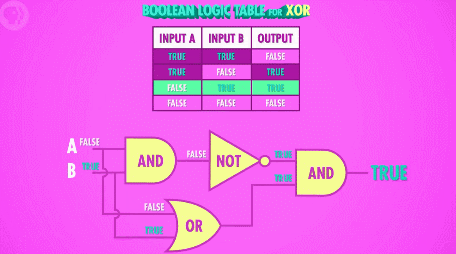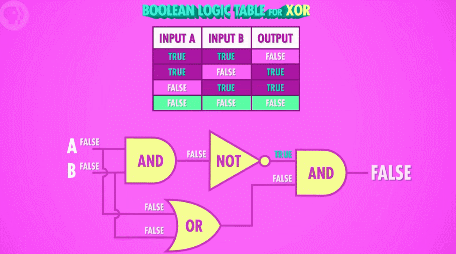
后面会提到,“异或”操作非常有用,所以工程师们将“异或”门抽象成了一个“笑脸”的符号 :)D ,这是新的一层抽象,赶快把它放进工具箱,再也不用关心它是由哪几个门电路或者多少个晶体管组成的了!
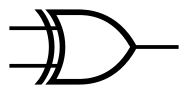
之后
从现在开始,我们终于用电信号来表示我们的数据(真、假)了。并且通过逻辑运算,我们能描述出较为复杂的逻辑,比如:如果小明在周末或情人节买了玫瑰与两张电影票等人看电影,那么小明谈恋爱了为真。
我们用二进制表述出了逻辑,接下来,我们将会看看二进制在计算机里是怎么表示、存储和计算的。